初始介绍
符号规定
在本文中,我们做如下规定:
Matrix矩阵为:$\mathbf{A}, \mathbf{X}, \mathbf{Y}$
Vector向量(规定为$\color{red} {列} $向量)为:$ \mathbf{a}, \mathbf{x}, \mathbf{y}$
Scalar标量为:$a, x, y$
分子布局
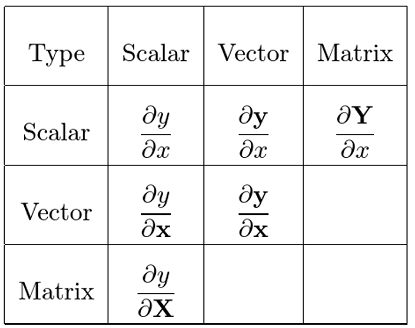
在矩阵求导中,我们有两种布局(分子与分母)
为了方便起见,本文只阐述了分子布局即:
$$\frac{\partial \mathbf{y}}{\partial {x}}=\left[\begin{array}{c} \frac{\partial y_{1}}{\partial x} \\ \frac{\partial y_{2}}{\partial x} \\ \vdots \\ \frac{\partial y_{m}}{\partial x}\end{array}\right]\ \ \
\frac{\partial y}{\partial \mathbf {x}} = \left[\frac{\partial y}{\partial x_{1}} ,\frac{\partial y}{\partial x_{2}}, \cdots ,\frac{\partial y}{\partial x_{n}}\right]$$
分母布局为分子布局的转置。
记忆方法:分子列向量分母标量,看作长筒冰淇淋,分母看作小盒子,“能站住”。分子标量分母列向量,则盒子把冰淇淋“压倒了”。或可看最后结果的行数,是分子的行数便是分子布局。
一般的,我们会遇到如下布局,且可用记忆方法配合右图形象理解(下面是结果):
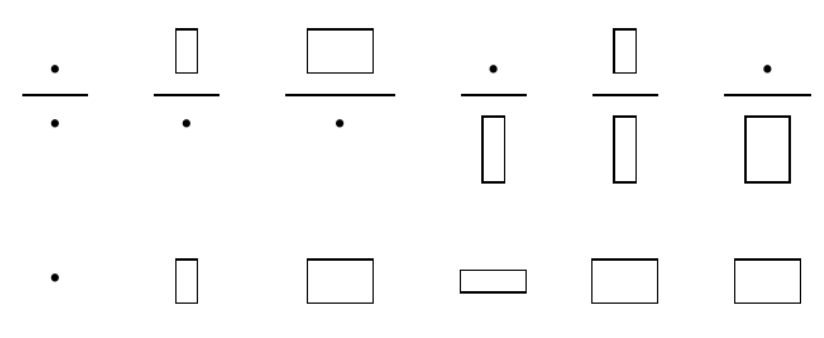
Vector-by-Vector
另外我们有:
$\mathbf{y}=\begin{bmatrix}
y_1 \\
y_2 \\
\vdots \\
y_m
\end{bmatrix}$
$\mathbf{x}=\begin{bmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{bmatrix}$
由 $ \frac{\partial \mathbf{y}}{\partial \mathbf{x}}$ 运算后产生m行n列矩阵:
$ \frac{\partial \mathbf{y}}{\partial \mathbf{x}} \stackrel{\text { def }}{=}\left[\begin{array}{cccc}\frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} & \ldots & \frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} & \ldots & \frac{\partial y_{2}}{\partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \frac{\partial y_{m}}{\partial x_{2}} & \ldots & \frac{\partial y_{m}}{\partial x_{n}}\end{array}\right] $
这种矩阵可被称为Jacobian matrix。
接下来举个例子,若我们有:
$$\mathbf{y}=\begin{bmatrix}
y_1 \\
y_2 \\
\end{bmatrix}
\ \ \ \mathbf{x}=\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}\ \ 且y_1=x^2_1-2x_2 \ ,\ y_2=x^2_3-4x_2$$
则能得到:
$$\frac{\partial \mathbf{y}}{\partial \mathbf{x}} =\begin{bmatrix}
2x_1 & -2 & 0 \\
0 & -4 & 2x_3 \\
\end{bmatrix}
$$
Matrix-by-Scalar
同样的,我们可以给出矩阵与向量间的运算关系:
$ \frac{\partial \mathbf{Y}}{\partial {x}} \stackrel{}{=}\left[\begin{array}{cccc}\frac{\partial Y_{11}}{\partial x} & \frac{\partial Y_{12}}{\partial x} & \ldots & \frac{\partial Y_{1n}}{\partial x} \\ \frac{\partial Y_{21}}{\partial x} & \frac{\partial Y_{22}}{\partial x} & \ldots & \frac{\partial Y_{2n}}{\partial x} \\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial Y_{m1}}{\partial x} & \frac{\partial Y_{m2}}{\partial x} & \ldots & \frac{\partial Y_{mn}}{\partial x}\end{array}\right]$
$ \ \ \ \ \ and \ \ \ \ \frac{\partial y}{\partial\mathbf{X}} \stackrel{}{=}\left[\begin{array}{cccc}\frac{\partial y}{\partial X_{11}} & \frac{\partial y}{\partial X_{21}} & \ldots & \frac{\partial y}{\partial X_{m1}} \\ \frac{\partial y}{\partial X_{12}} & \frac{\partial y}{\partial X_{22}} & \ldots & \frac{\partial y}{\partial X_{m2}} \\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial y}{\partial X_{1n}} & \frac{\partial y}{\partial X_{2n}} & \ldots & \frac{\partial y}{\partial X_{mn}}\end{array}\right] $
可以注意到当矩阵在分母时$\mathrm{X}$已经“被转置”
常用求导公式
注:其中$\mathbf{a},\mathrm{A}$都不是$\mathbf{x}, \mathrm{X}$的函数
$$\frac{\mathrm{d} \mathbf{a}}{\mathrm{d} x} =\mathbf{0} \tag{1} \qquad (column \ matrix)$$
$$\frac{\mathrm{d}a }{\mathrm{d} \mathbf{x}} =\mathbf{0}^{\mathrm{T}} \tag{2} \qquad (row \ matrix)$$
$$\frac{\mathrm{d}a }{\mathrm{d} \mathbf{X}} =\mathbf{0}^{\mathrm{T}} \tag{3} \qquad (matrix)$$
$$\frac{\mathrm{d} \mathbf{a} }{\mathrm{d} \mathbf{X}} =\mathbf{0} \tag{4} \qquad (matrix)$$
$$\frac{\mathrm{d} \mathbf{x} }{\mathrm{d} \mathbf{x}} =\mathbf{I} \tag{5} \qquad (matrix)$$
若想从“直观上”理解结果为什么会有转置符,可以反复理解 (1.2)分子布局 中的右图
$$\frac{\mathrm{d} \mathbf{a}^{\mathrm{T}}\mathbf{x} }{\mathrm{d} \mathbf{x}}=\frac{\mathrm{d} \mathbf{x}^{\mathrm{T}}\mathbf{a} }{\mathrm{d} \mathbf{x}}=\mathbf{a}^{\mathrm{T}} \tag{6} $$
$$\frac{\mathrm{d} \mathbf{x}^{\mathrm{T}}\mathbf{x} }{\mathrm{d} \mathbf{x}}=2\mathbf{x}^{\mathrm{T}} \tag{7} $$
$$\frac{\mathrm{d} ({\mathbf{x}^{\mathrm{T}}\mathbf{a}})^2 }{\mathrm{d} \mathbf{x}}=2\mathbf{x}^{\mathrm{T}}\mathbf{a}\mathbf{a}^{\mathrm{T}} \tag{8} $$
$$\frac{\mathrm{d} \mathbf{Ax} }{\mathrm{d} \mathbf{x}} =\mathbf{A} \tag{9} $$
$$\frac{\mathrm{d} \mathbf{x}^{\mathrm{T}}\mathbf{A} }{\mathrm{d} \mathbf{x}}=\mathbf{A}^{\mathrm{T}} \tag{10} $$
$$\frac{\mathrm{d} \mathbf{x}^{\mathrm{T}}\mathbf{A}\mathbf{x} }{\mathrm{d} \mathbf{x}}=\mathbf{x}^{\mathrm{T}}(\mathbf{A}+\mathbf{A}^{\mathrm{T}}) \tag{11} $$
注:其中(11)用到了矩阵求导中的"莱布尼兹法则"(仔细思考前者的行列与后者的行列就可以明白): $$\frac{\partial \mathbf u^{\mathrm{T} }\mathbf v}{\partial \mathbf x} = \mathbf u^{\mathrm{T}} \frac{\partial \mathbf v}{\partial \mathbf x} + \mathbf v^{\mathrm{T}}\frac{\partial \mathbf u}{\partial \mathbf x}$$
实例练习
我们会好奇一个问题:为什么大多数求导后以及求导时形式都是转置在前?
可以这么理解,假设有参数$\mathbf{\Theta } =\begin{bmatrix}
\theta_0\\
\theta_1\\
\theta_2
\end{bmatrix}$
以及列向量$\mathbf{x}=\begin{bmatrix}
1 \\
x_1 \\
x_2
\end{bmatrix}$
我们可以把多元函数表达为$$f(x_1,x_2)=\Theta^{\mathrm{T}} \mathbf{x}=\theta_0 + \theta_1x_1 + \theta_2x_2$$
方便计算,且符合目的。在计算结果直觉中一定要紧紧把握结果与分子(上下拉长)分母(左右拉宽)的关系。
多元线性回归推导
在西瓜书第三章开头中,我们需要求解最小error$\ E=(\boldsymbol{y}-\mathbf{X}\boldsymbol{\hat{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X}\boldsymbol{\hat{w}}) $ 对其展开有:$$ \begin{aligned}(\boldsymbol{y}-\mathbf{X}\boldsymbol{\hat{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X}\boldsymbol{\hat{w}}) &=(\boldsymbol{y}^{\mathrm{T}}-\boldsymbol{\hat{w}}^{\mathrm{T}}\mathbf{X}^{\mathrm{T}})(\boldsymbol{y}-\mathbf{X}\boldsymbol{\hat{w}}) \\ &= \boldsymbol{y}^{\mathrm{T}} \boldsymbol{y}- (\boldsymbol{y}^{\mathrm{T}} \mathbf{X}) \boldsymbol{\hat{w}}-\boldsymbol{\hat{w}}^{\mathrm{T}} (\mathbf{X}^{\mathrm{T}} \boldsymbol{y}) +\boldsymbol{\hat{w}}^{\mathrm{T}} (\mathbf{X}^{\mathrm{T}} \mathbf{X}) \boldsymbol{\hat{w}} \end{aligned}$$
把括号中看作常数,每一项分别对 $\boldsymbol{\hat{w}}$ 求导,利用公式$(9),(10),(11)$可得:
$$ \frac{\partial \boldsymbol{E}_{\boldsymbol{\hat{w}}} }{\partial \boldsymbol{\hat{w}}} = -\boldsymbol{y}^{\mathrm{T}} \mathbf{X} - \boldsymbol{y}^{\mathrm{T}} \mathbf{X} + \boldsymbol{\hat{w}}^{\mathrm{T}} [\mathbf{X}^{\mathrm{T}} \mathbf{X}+(\mathbf{X}^{\mathrm{T}} \mathbf{X})^{\mathrm{T}}] = -2\boldsymbol{y}^{\mathrm{T}} \mathbf{X} + 2\boldsymbol{\hat{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \mathbf{X} $$
令其等于零可得:
$$\boldsymbol{y}^{\mathrm{T}} \mathbf{X} = \boldsymbol{\hat{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \mathbf{X}$$
同时转置可得:
$$ \mathbf{X}^{\mathrm{T}} \boldsymbol{y} = \mathbf{X}^{\mathrm{T}} \mathbf{X} \boldsymbol{\hat{w}} $$
若此时 $\mathbf{X}^{\mathrm{T}} \mathbf{X}$ 为满秩、非奇异矩阵,我们可以得到:
$$\boldsymbol{\hat{w}}=( \mathbf{X}^{\mathrm{T}} \mathbf{X})^{-1} \mathbf{X}^{\mathrm{T}} \boldsymbol{y} \\ \ \\ Q.E.D$$
上文公式的证明过程
- 如果你不知道计算结果是否正确,可以使用验算矩阵求导结果是否正确进行验证。
-
证明(6) $$ Let \; s=\boldsymbol{a}^T\mathbf{x}={a}_1x_1+\cdots +a_nx_n.\quad Then,\;\frac{\partial s}{\partial x_i}=a_i \\ So,\:\frac{\mathrm{d} \boldsymbol{a}^{\mathrm{T}}\mathbf{x} }{\mathrm{d} \mathbf{x}}=\frac{\mathrm{d} s}{\mathrm{d} \mathbf{x}}=\left[ \frac{\mathrm{d}s}{\mathrm{d}x_1},\frac{\mathrm{d}s}{\mathrm{d}x_2},\cdots ,\frac{\mathrm{d}s}{\mathrm{d}x_n} \right] =\left[ a_1,a_2,\cdots ,a_n \right] =\boldsymbol{a}^T $$
-
证明(7) $$ Let \; s=\boldsymbol{\mathbf{x}}^{\mathrm{T}}\mathbf{x}=\sum_i{x_{i}^{2}}. \quad Then,\;\frac{\partial s}{\partial x_i}=2x_i \\ So, \;\; \frac{\mathrm{d} s}{\mathrm{d} \mathbf{x}}=2\mathbf{x}^{\mathrm{T}} $$
-
证明(8)
当成复合函数即可,相信你可以自己证明! -
证明(9)
比较麻烦的方法,由: $$ \mathbf{A}\mathbf{x}=\left[ \begin{matrix} a_{11}& \cdots& a_{1n}\\ \vdots& \ddots& \vdots\\ a_{n1}& \cdots& a_{nn}\\ \end{matrix} \right] \left[ \begin{array}{c} x_1\\ \vdots\\ x_n\\ \end{array} \right] =\left[ \begin{array}{c} a_{11}x_1+\cdots +a_{1n}x_n\\ \vdots\\ a_{n1}x_1+\cdots +a_{nn}x_n\\ \end{array} \right] $$
再由“分子决定行,分母决定列,分别求导”原则(如果不理解可以返回开头再看一遍) 得到: $$ \left[ \begin{matrix} a_{11}& \cdots& a_{1n}\\ \vdots& \ddots& \vdots\\ a_{n1}& \cdots& a_{nn}\\ \end{matrix} \right]=\mathbf{A} $$ 比较简单的方法:(类似上面的证明)
$$ Let\,\, \boldsymbol{s}=\mathbf{A} \mathbf{x}. \;\; Then, s_i=\sum_j{\begin{array}{c} a_{ij}x_j\\ \end{array}}, and\,\,\frac{\partial s_i}{\partial x_j}=a_{ij}. \\ So, \frac{\mathrm{d} \boldsymbol{s}}{\mathrm{d} \mathbf{x}}=A. $$
注释:有些情况(比如矩阵对向量、向量对矩阵、矩阵对矩阵求导)可能存在不好表达的情况(详情参考Reference4)因为列向量对列向量求导本质是用雅可比矩阵定义的。在这里建议直接记住结果,或者用网站验证结果;如果会用张量指标计算也行。如果你想学习更一般地做法,可以参考附录3的文章。